可持久化数据结构学习笔记

发表于 分类于 ， ， 阅读次数： 本文字数： 5k 阅读时长 ≈ 5 分钟
水母中学好耶

水母中学好耶。

几个基础概念

  1. 可持久化：对于一个数据结构，需要维护其所有的历史版本

  2. 部分可持久化：对于一个历史版本，允许访问，不能修改

  3. 完全可持久化：对于一个历史版本，可访问可修改

  4. （这个以前完全不知道）Confluent persistent（我的翻译：合并式可持久化）：允许合并历史版本，不太能维护（不常见）

可持久化线段树

最朴素的，每次复制一整棵树。

然而空间和时间都无法接受。

于是，我们考虑优化。

有一张直观的图：

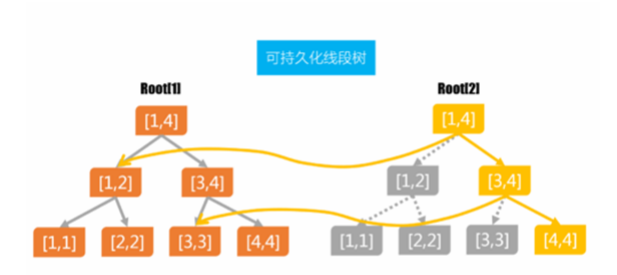
注意到，每次最多有 \(\log n\) 个节点被改了。没改的连到历史版本对应节点，于是解决。

每次要新开根节点，一是要修改，二是操作时方便找。

空复时复都是 \(O(m\log n)\)（\(m\) 是操作次数），可以接受。

这种方法被称作“path copy”，但中文译名暂无。我觉得可以译为“懒惰连边”。

下面的代码是教练课件中的实现代码：

1
2
3
4
5
6
7
8
9
10
11
void Insert(int l,int r,int d,int &rt,int lrt){
  rt=++tnt;t[rt]=t[lrt];
  if(l==r){
    //处理
    return;
  }
  int mid=l+r>>1;
  if(mid>=d)Insert(l,mid,d,t[rt].lson,t[lrt].lson);
  else Insert(mid+1,r,d,t[rt].rson,t[lrt].rson);
  update(rt,l,r);
}

标记永久化

区间修改，我们会打懒标记 lazy-tag。

然而可持久化线段树下放的话，很麻烦。

这时我们就可以用“标记永久化”，顾名思义，就是把标记打在节点上后不进行下放，而是在查询这个节点的值的 时候再考虑这个标记。然后就解决了。

一道例题

这个问题能直观地看出可持久化有多好用。

区间第 \(k\) 小值问题：给定一个序列，多次查询其中某个区间的第 \(k\) 小值。

首先想到二分。

然后 check 函数统计有多少个数小于等于它。

可以用整体二分或者可持久化线段树实现。

  1. 整体二分

优点：空间线性，支持单点修改

缺点：离线，复杂度多个 \(\log\)，难理解

没学过，不细讲。

时间复杂度 \(O((n+m)\log^2 n)\)，空间复杂度 \(O(n+m)\)。

  1. 可持久化线段树

优点：在线，复杂度少个 \(\log\)，好写

缺点：空间多个 \(\log\)，不能修改

从 \(1\) 到 \(n\) 建出每个前缀的权值线段树，然后用可持久化线段树。

查询就直接线段树上二分，再用前缀和基础知识。

时间复杂度 \(O((n+m)\log n)\)，空间复杂度 \(O(n\log n)\)。

优劣对比：

各自优一个 \(\log\)，所以要具体题目具体分析。

但是可持久化线段树的支持在线是真的实用。

一些可持久化数据结构

可持久化 trie 树

观察到 trie 树是树。

所以可以用 path copy。

可持久化平衡树

treap 不太能（也许是不能）可持久化。

于是，我们可以想到 无旋/分裂/FHQ treap。

这样，就可以用 path copy 了。

可持久化可并堆

不知道这是啥。教练说可以用左偏树，也不知道是啥。确实需要多学一些知识。

用了左偏树，还是照抄 path copy。

我们会发现，path copy 不是一点的好用，而是常用、非常好用、好理解、好写的可持久化神兵。

其他的可持久化数据结构

复杂度不依赖均摊（反例：splay）的，大多数都可以用 path copy。

为什么类似 splay 的数据结构不能？

因为均摊。

如果我出个数据，疯狂卡你的 splay，而且每次历史版本都访问你被卡的版本，你就 TLE 了。

当然，也不是说他们不行，部分依赖均摊的也能用 path copy。只不过只能做到部分可持久化。

例题

  1. P3919

模版题，结合代码讲。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL int
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define i128 LL
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
//比较奇怪的一点：要用快读快写。不知道为啥。
void read(i128 &x)
{
	i128 f=1;
	x=0;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=x*10+ch-'0';
		ch=getchar();
	}
	x*=f;
}
void writing(i128 x)
{
	if(x>=10)writing(x/10);
	putchar(x%10+'0');
}
void write(i128 x)
{
	if(x<0)
	{
		putchar('-');
		x=-x;
	}
	writing(x);
}
LL n,m,tot,head[N],a[N];
struct node
{
	LL l,r,ls,rs,val;//区间左右端点，左右儿子，值
}t[N*30];//因为很多版本，开大一点
inline LL newnode(LL l,LL r)
{
	t[++tot]=(node){l,r,0,0,0};
	return tot;
}//动态开点
void build(LL k)
{
	LL l=t[k].l,r=t[k].r;
	if(l==r)
	{
		t[k].val=a[l];
		return;
	}
	LL mid=l+r>>1;
	t[k].ls=newnode(l,mid);
	t[k].rs=newnode(mid+1,r);
	build(t[k].ls);
	build(t[k].rs);
}
LL newver(LL k,LL x)//新版本
{
	if(!k)return 0;
	if(x<t[k].l||x>t[k].r)return k;
	LL p=newnode(t[k].l,t[k].r);
	t[p]=t[k];
	t[p].ls=newver(t[k].ls,x);
	t[p].rs=newver(t[k].rs,x);
	return p;
}
void modify(LL k,LL x,LL val)
{
	if(t[k].l>x||t[k].r<x)return;
	if(t[k].l==x&&x==t[k].r)
	{
		t[k].val=val;
		return;
	}
	modify(t[k].ls,x,val);
	modify(t[k].rs,x,val);
}
LL query(LL k,LL x)
{
	if(t[k].l==x&&x==t[k].r)return t[k].val;
	LL mid=t[k].l+t[k].r>>1;
	if(x<=mid)return query(t[k].ls,x);
	return query(t[k].rs,x);
}
int main()
{
	read(n);
	read(m);
	rep(i,1,n,1)read(a[i]);
	head[0]=newnode(1,n);
	build(head[0]);
	rep(i,1,m,1)
	{
		LL ver,op,x,val;
		read(ver);
		read(op);
		read(x);
		head[i]=newver(head[ver],x);
		if(op==1)
		{
			read(val);
			modify(head[i],x,val);
		}
		else
		{
			write(query(head[i],x));
			putchar('\n');
		}
	}
	return 0;
}

确实很简单。\(100\) 多行，我还写了很多的 #define。

  1. P2839

首先，我们得知道如何做某一次的询问。

一个常见的中位数套路是二分，把 \(<mid\) 的看做 \(-1\)，否则看做 \(1\)，若某段的和 \(\ge 0\) 则中位数 \(\ge mid\)。

（如果看到“主席树”看不懂的，请牢记这就是可持久化权值线段树。）

用主席树维护，初始每个位置都是 \(1\)，按照权值大小从小到大变 \(-1\)。

然后，我们可以想到维护其前缀和。时间复杂度骤降。

询问时，如上去二分，然后找到 \([a-1,b-1]\) 里权值最小的位置和 \([c,d]\) 中权值最大的位置。

再然后看看其区间和是否 \(\ge 0\)，时间复杂度 \(O((n+m)\log^2 n)\)。

  1. 火车管理

感觉这个比 T2 简单诶。

先建立一个可持久化线段树，维护每个铁路每个时间的栈顶的吨位和栈顶火车的入栈时间。

再维护一颗线段树用来统计答案。

然后，就简单了：

  • 1 操作：直接在答案线段树里询问即可。

  • 2 操作：可持久化线段树记录了入栈时间，所以我们删完后再用可持久化线段树查出当前入栈之前的栈顶的信 息即可（可持久化的优势就体现了），然后在答案线段树上和可持久化线段树上修改。

  • 3 操作：在可持久化线段树上区间覆盖，区间覆盖算是个很基础的 trick 了，然后在答案线段树上修改。

时间、空间复杂度均为 \(O(n\log n)\)。

  1. CF464E

请注意，截止该文章发布前，CF 开了 CF 导致洛谷 RMJ 无法正常使用。建议去 CF 原站提交（但是去原站也有被 CF 盾墙掉的问题）。等等吧。

首先明确，我们要用 dijkstra 求最短路。因为 SPFA 被卡了，详见https://www.luogu.com.cn/discuss/780372。

对于最短路的长度，维护一棵线段树，下标为二进制位。

比较可以通过线段树二分找出首个不同的位，判断两个线段树结点是否相同可以用哈希（二进制，模数 \(1000000007\) 即可，因为此时输出答案直接输出其哈希值）。

加 \(1\) 可以相当于把若干个连续的 \(1\) 变成 \(0\)，然后把下一位变成 \(1\)。

教练课件上写“可以通过线段树上二分找出极长的 \(1\) 连续段然后进行修改。”，感觉没直接搞简便。

使用可持久化线段树，从上一个版本继承过来，以保证不会超时。

总结

可持久化线段树非常万金油，图论都能用。当然其他的也有用。限于篇幅和水平，还有很多（比如可持久化并查集）没放上来。

很感谢水母中学，以前只知道可持久化是“记录变化”，现在看看，不是这么简单的。