单调队列 & 斜率优化 DP 学习笔记

UpDate on 2024/5/23 代码增加一点注释

UpDate on 2024/5/28 增加一个同学写的反思

UpDate on 2024/5/29 写完单调队列优化多重背包部分

UpDate on 2024/5/31 单调队列优化多重背包部分添加代码

单调队列优化 DP

单调队列

注意，其与优先队列不是同一种数据结构。（其实也不是严格的队列）

其模板题。

每当一个新的数加入，当队尾大于等于/小于等于（取决于每一道题目）这个数时，弹出队尾（因此这不是严格的队列）并继续比较直到队尾不满足其大于等于/小于等于这个数或队列空。然后将这个数加入队尾。

还有一个操作：当队头不优时，弹出队头。

似乎无法优化 DP？

例题

状态设计可以想到是当放第 \(i\) 个烟花的时候你在 \(j\) 位置能获得的最大开心度。

转移方程依据题意，是 \[ f_{i,j}=\max\lbrace f_{i-1,k}+b_i-|a_i-j|\rbrace \]

此处 \(k\) 范围

\[ j-(t_i-t_{i-1})\times d\le k \le j+(t_i-t_{i-1})\times d \]

然而会超时，考虑优化。

但是，这坨式子很明显无法单调队列优化，其他优化似乎也不行。

一个想法

暴力是三层循环，第一层 \(i\)，第二层 \(j\)，第三层 \(k\)（因为 \(i\) 和 \(j\) 决定 \(k\) 的范围）。

转移在 \(k\) 层进行。

此时 \(i\) 和 \(j\) 已经固定，所以： \[ f_{i,j}=\max\lbrace f_{i-1,k}\rbrace+b_i-|a_i-j| \] 既然 \(+b_i-|a_i-j|\) 影响单调队列，我们就提出去！

于是时间复杂度降到 \(O(nm)\)。

code from OI-wiki

#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;

const int maxn = 150000 + 10;
const int maxm = 300 + 10;

ll f[2][maxn];
ll a[maxm], b[maxm], t[maxm];
int n, m, d;

int que[maxn];

int fl = 1;

void init() {
  memset(f, 207, sizeof(f));
  memset(que, 0, sizeof(que));
  for (int i = 1; i <= n; i++) f[0][i] = 0;
  fl = 1;
}

void dp() {
  init();
  for (int i = 1; i <= m; i++) {
    int l = 1, r = 0, k = 1;
    for (int j = 1; j <= n; j++) {  // 在这里使用了单调队列的优化，推式子详见上面
      for (; k <= min(1ll * n, j + d * (t[i] - t[i - 1])); k++) {
        while (l <= r && f[fl ^ 1][que[r]] <= f[fl ^ 1][k]) r--;
        que[++r] = k;
      }

      while (l <= r && que[l] < max(1ll, j - d * (t[i] - t[i - 1]))) l++;
      f[fl][j] = f[fl ^ 1][que[l]] - abs(a[i] - j) + b[i];
    }

    fl ^= 1;
  }
}

int main() {
  cin >> n >> m >> d;
  for (int i = 1; i <= m; i++) cin >> a[i] >> b[i] >> t[i];

  // then dp
  dp();
  ll ans = -1e18;
  for (int i = 1; i <= n; i++) ans = max(ans, f[fl ^ 1][i]);
  cout << ans << endl;
  return 0;
}

多重背包的单调队列优化

写一些我的见解吧。

这应该是多重背包的最优解了。

例题。

我们知道，暴力的转移方程是：

\[ dp_j=max\{dp_{j-kc_i}+kw_i\} \]

其中 \(1\le k \le min\{m_i,\frac{j}{c_i}\}\)。

特别提一下，我这里的各个变量和数组与原题不同，物品个数是 \(n\)，体积是 \(c_i\)，价值是 \(w_i\)，有 \(m_i\) 个，背包大小是 \(C\)。

打暴力的代码的话，是三层循环，我们发现 \(i,j\) 之间没有关系，但是 \(j,k\) 有关系，\(k\) 在 \(j\) 上有滑动窗口。

看似无法应用单调队列。

但是，我们发现：\(j+m\times c_i=j+(m+p)\times c_i-p\times c_i\)。

所以我们可以想到，当某些 \(j\) 除以某个 \(c_i\) 的余数相同时，他们的 \(k\) 会有重叠。

那么，我们设 \(j=yc_i+b\)，其中 \(b\) 为余数（\(j\bmod c_i\)），\(y=\lfloor\frac{j}{c_i}\rfloor\)。

带入，原方程变为：

\[ dp_{yc_i+b}=max\{dp_{b+(y-k)c_i}+kw_i\} \]

我们发现它看上去还是不能优化。

然而我们可以令 \(x=y-k\)，此时方程变为：

\[ dp_{yc_i+b}=max\{dp_{b+xc_i}-xw_i+yw_i\} \]

然后就能单调队列优化了。

code by whl(I improved its code style and added some annotations)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N=4e4+10;
LL n,m,v,w,c,q[N],hh,tt,f[N],g[N];
int main()
{
    scanf("%lld%lld",&n,&m);
    while(n--)//输入时直接处理
    {
        scanf("%lld%lld%lld",&v,&w,&c);
        memcpy(g,f,sizeof(f));//滚动数组的一种实现方式，上文的方程等都用了滚动数组
        for(int i=0;i<w;i++)//余数，所以是 [0,w)
        {
            hh=0;
            tt=-1;
            //单调队列，这样等价于 h=1,t=0
            for(int j=i;j<=m;j+=w)//将这个余数的所有状态更新
            {
                while(hh<=tt&&q[hh]<j-w*c)hh++;//个数超了 c
                while(hh<=tt&&g[q[tt]]-v*q[tt]/w<=g[j]-v*j/w)tt--;//队尾没有 j 优
                q[++tt]=j;
                f[j]=g[q[hh]]+v*((j-q[hh])/w);//转移
            }
        }
    }
    printf("%lld",f[m]);
    return 0;
}

斜率优化！（参考了罗勇军、郭卫斌的《算法竞赛》）

有一种 DP 转移方程： \[ dp_i=\min\{dp_j-a_id_j\}(0\le j<i,d_j\le d_{j+1},a_i\le a_{i+1}) \] 朴素的去 DP，\(O(n^2)\)。

转换

把 \(i\) 看作不变的常量。

把除了 \(dp_i\) 以外的所有与 \(i\) 有关的项看作常量。

把 \(j\) 看作变量。

要求 \(j\) 变化时 \(dp_i\) 的最优值。

把 \(\min\) 去掉，就变成了： \[ dp_j=a_id_j+dp_i \] 为了让它看着像一次函数（才能求斜率），设 \(y=dp_j,x=d_j,k=a_i,b=dp_i\)。

原式变为 \(y=kx+b\)。

斜率优化需要满足几个条件：

1. \(x\) 和 \(y\) 与 \(j\) 有关，且只有 \(y\) 中包含 \(dp_j\)。于是 \((x,y)\) 这个点就是一种决策。

2. 斜率 \(k\)、截距 \(b\) 与 \(i\) 有关，并且只有 \(b\) 中含 \(dp_i\)，其中最小的 \(b\) 包含最小的 \(dp_i\)，也就是转移方程的解。

\((x_1,y_1)\) 和 \((x_2,y_2)\) 这两个点组成的直线的斜率为 \((y_2-y_1)/(x_2-x_1)\)，我们会发现这个斜率只与 \(j\) 有关，于是可以用单调队列！

还有一点，\(x\) 与 \(k\) 要单调增加。

具体来说：\(x\) 随 \(j\) 递增而递增，\(k\) 随 \(i\) 递增而递增。

求某个 \(dp_i\)

我们要求最优点，设它为 \(v\)。

利用“下凸壳”。

如果这次转移的各个点（决策）是这样的：

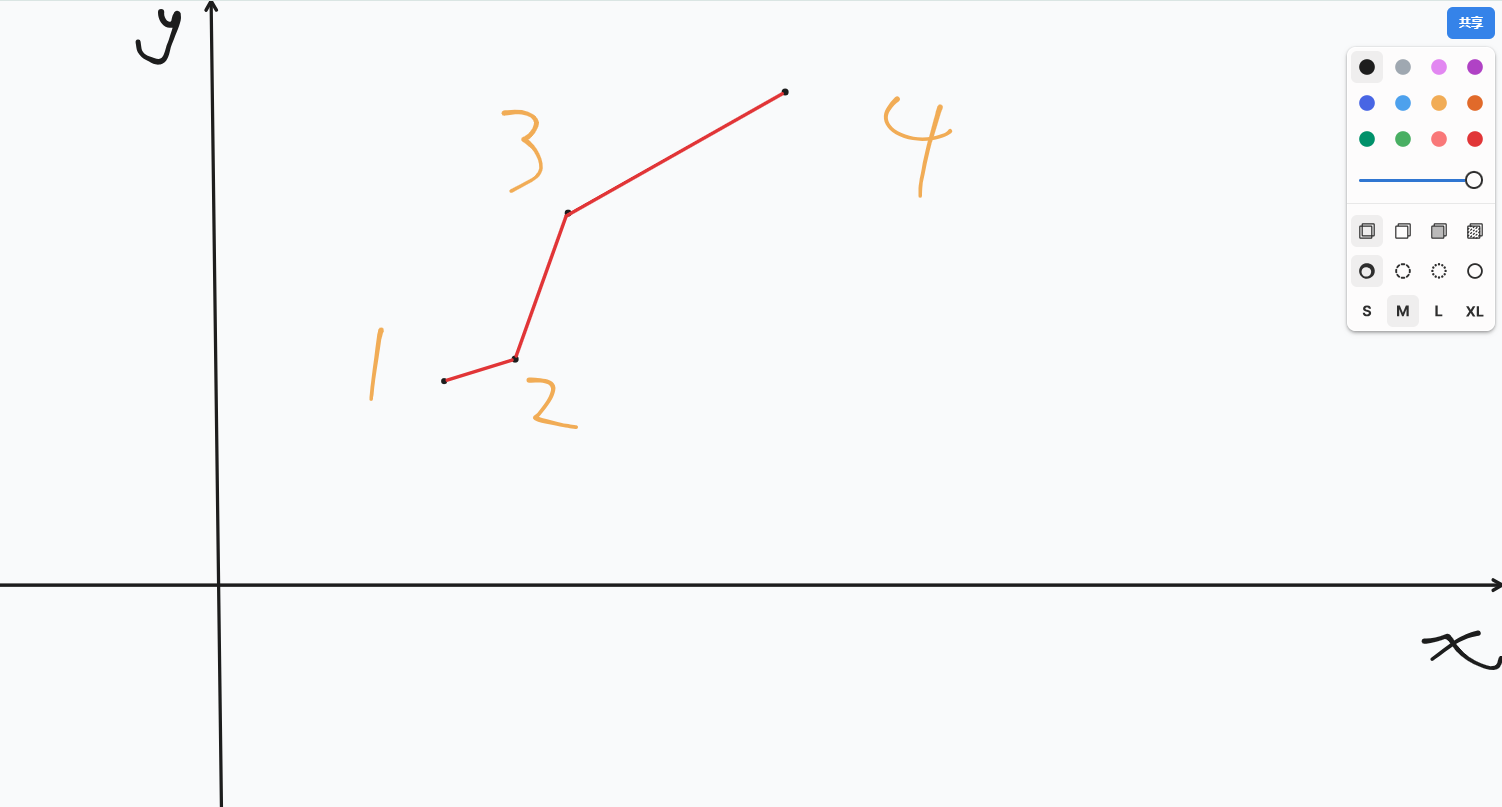
上凸壳就是 \(2,3,4\)。

我们可以发现：经过上凸壳中间那个点（即 \(3\)）的直线的截距（\(b\)）一定大于（《算法竞赛》中此处为“小于”，应为笔误）\(2\) 和 \(4\) 的直线的截距，于是 \(3\) 一定不是最终的最优的点，去掉（绿色代表删掉了）：

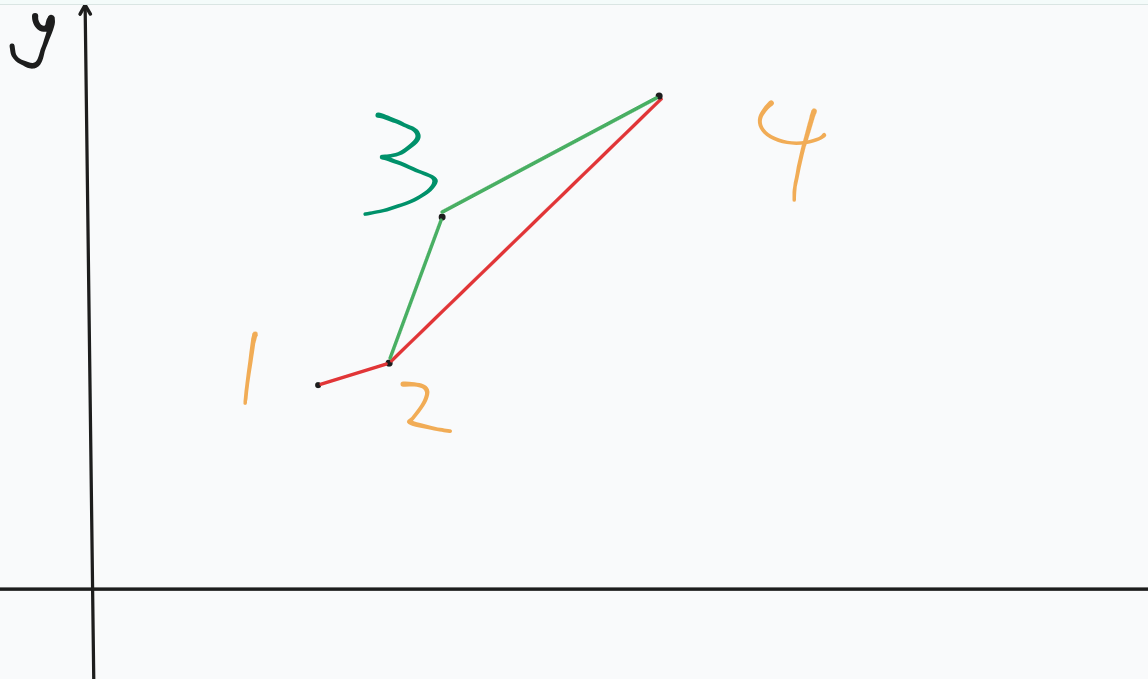
剩的点都满足下凸壳关系（\(12\) 的斜率小于 \(24\) 的斜率）。

假设在这里面 \(12\) 的斜率小于 \(k\)，\(34\) 的斜率大于 \(k\)，那么最优点就是 \(2\)（如下图，蓝色直线即为斜率为 \(k\) 的直线）。

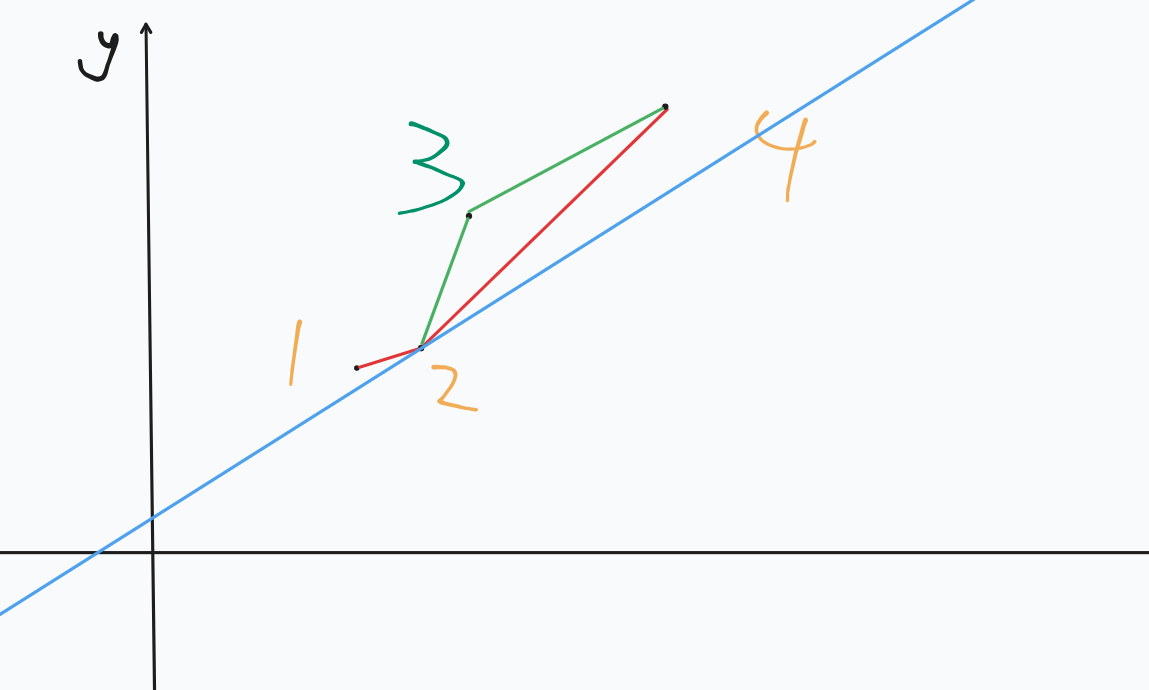
我们发现这部分用单调队列做非常容易。

入队

我们现在要处理一个斜率：\((y_2-y_1)/(x_2-x_1)\)。

斜率要单调上升，因为是下凸壳。

如果准备进队了发现斜率不单调上升，就把前面弹走。

每次进队后就大致像下图的结构（By OI Painter）：

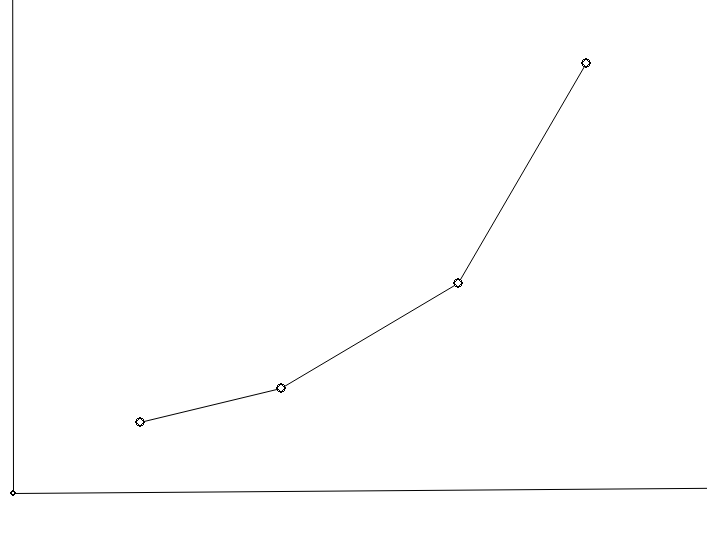
出队

注意，这说的是前面提到的“当队头不优时，弹出队头”。

设队头的两个点分别是 \(v_1\) 和 \(v_2\)。

如果 \(v_1v_2\) 这条线段的斜率小于等于（我认为此处应该有等于，因为我们的条件是“左边的斜率小于 \(k\)，右边的的斜率大于 \(k\)”） \(k\)，就可以把 \(v_1\) 弹出去了（如上，不可能最优）。

然后一直弹，弹到 \(v_1v_2\) 这条线段的斜率大于 \(k\)，此时队头就是这个 \(dp_i\) 的最优点。

（快速地）求所有的 \(dp_i\)

然而我们会发现一个显著的问题：

问题

求一个 \(dp_i\) 是 \(O(n)\) 的。

求所有的是 \(O(n^2)\) 的。

那这和暴力似乎没有区别。

我们来列一下各个 \(dp_i\) 要处理的决策点：

举个例子，有两个数，\(j\) 和 \(o\)。

不妨设 \(j<o\)。

\(dp_j\) 要处理的之前的决策点是：

\[ {v_0,v_1,\dots,s_j} \]

\(dp_o\) 要处理的之前的决策点是：

\[ {v_0,v_1,\dots,s_j,\dots,s_o} \]

前面的 \({v_0,v_1,\dots,s_j}\) 是重复的，可以避免这些重复的扫描。

方法

《算法竞赛》上我觉得讲麻烦了，我讲一下我的想法：

我们前文保证过“\(x\) 与 \(k\) 单调增加”，于是 \(k_o\) 的斜率一定大于 \(k_j\) 的。

于是我们只用一个单调队列从头到尾处理即可，每次处理完剩下的数据后一个位置还能用。

时间复杂度骤降至 \(O(n)\)。

核心代码如下：

main code

for(int i=1;i<=n;i++)
{
    while(h<t&&slope/*斜率函数，但这个词一般表示“斜坡”*/(q[h],q[h+1])<k)h++;
    dp[i]=/*状态转移方程*/;
    while(h<t&&slope(i,q[t-1])<slope(q[t-1],q[t]))t--;
    q[++t]=i;
}

然而我想说点有关代码的事：

既然写到了代码

首先要有一个良好的代码习惯，比如记住上面那个代码，当作模板；

第二是我个人倡导的把大括号写开，即：

for(/*...*/)
{
    /*do sth*/
}

而不是用

for(/*...*/){
    /*do sth*/
}

或者其他难以找到这个大括号对应的前面的或后面的在哪、难以调试的代码风格。

这样可以更好地调试，也可以有更好的心态（这是作为 OIer 很重要的一点）。

第三就是如果遇到毒瘤出题人卡精度，使用 slope 会有精度误差时，可以像我的同学 ly 那样写一个 slope_fz 和 slope_fm 函数，比较时就交叉相乘。

例题

设 \(f_i\) 表示输出前 \(i\) 个单词的最少费用，那么根据题意，我们设 \(s_i\) 表示前 \(i\) 个单词的费用之和。

转移方程就是：

\[ dp_i=\min\{dp_j+(s_i-s_j)^2+M\} \]

其中 \(1\le j<i\)。

中间过程大致如下：

展开、移项（对照 \(y=kx+b\) 的格式和要求），得：

\[ dp_j+{s_j}^2=2s_is_j+dp_i-{s_i}^2-M \]

那么，\(y\) 是 \(dp_j+{s_j}^2\)，\(x\) 是 \(2s_j\)，\(k\) 是 \(s_i\)，\(b\) 是 \(dp_i-{s_i}^2-M\)，而且符合条件。

code by ly（I solved the bugs）

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+100;
typedef long long ll;
ll n,m,q[N],l,r;
ll a[N],dp[N];
ll get_x(ll x)
{
	return 2*a[x];//即 2*s[j]
}
ll get_y(ll x)
{
	return dp[x]+a[x]*a[x];//即 dp[j]+s[j]*s[j]
}
ll slope_fz(ll x,ll y)
{
	return get_y(x)-get_y(y);//斜率的分子
}
ll slope_fm(ll x,ll y)
{
	return get_x(x)-get_x(y);//斜率的分母
}
int main()
{
	while(cin>>n>>m)
	{
		l=0;
		r=0;
		memset(dp,0,sizeof(dp));
		memset(q,0,sizeof(q));
		for(int i=1;i<=n;i++) 
		{
			scanf("%lld",&a[i]);
			a[i]+=a[i-1];
		}
		for(int i=1;i<=n;i++)
		{
			while(l<r&&slope_fz(q[l+1],q[l])<=(__int128)a[i]*slope_fm(q[l+1],q[l])) l++;
			dp[i]=dp[q[l]]+m+(a[i]-a[q[l]])*(a[i]-a[q[l]]);//注意，转移时还是按原转移方程进行转移
			while(l<r&&(__int128)slope_fz(i,q[r])*slope_fm(q[r],q[r-1])<=(__int128)slope_fz(q[r],q[r-1])*slope_fm(i,q[r])) r--;
			q[++r]=i;
		}
		printf("%lld\n",dp[n]);
	}
	return 0;
}

斜率优化的代码特别容易踩坑。

具体我目前知道的有：

1. 数据卡精度

• 方法一
• 方法二

开 long double 或者写高精度，不推荐。

但一般不卡精度时直接除就可以了。

像上文的代码那样写一个分子函数一个分母函数，比较时交叉相乘，但一定要注意不等号反向的问题！

同时还能解决分母可能为 $ 0 $ 的问题。

2. 单调队列写挂（即我解决的 bug）（解决方案：写成上文代码那样的初始 l=r=0 用时 l<r 单调队列，或者这么写，见下：）

/*初始化*/
l=1;
r=0;
q[++l]=0;
/*用的时候*/
l<=r

原因见此。

小结

斜率优化可以算是比较高级的 DP 优化了。

有些别的优化时间复杂度比斜率优化劣，比如笔者 2024.5.19 写的一道题，四边形不等式 \(O(n\log n)\)，而斜率优化 \(O(n)\)。

也可以找些习题进行练习，如 https://www.luogu.com.cn/problem/P5785 等。

另，由于本博客成文时间仓促，可能会有些错误，欢迎指出。

致谢

我学校的信息学教练 zxc，为此文提供了基础；

OI-wiki 斜率优化、单调队列优化部分编写人员及 OI-wiki 建设者，为本文提供代码及部分参考；

同学 whl，专门给我讲了一次斜率优化，并在 2024/5/31 提供单调队列优化多重背包例题代码；

同学 ly，提供例题代码（虽然我改了一点）、经典错误和其解决方案和反思；

OI Painter 开发者 EternalAlexander，提供一张图片的绘画支持；

tldraw 开发者，提供三张图片的绘画支持；

AcWing 站长 yxc，提供例题；

罗勇军、郭卫斌及其他《算法竞赛》编写、贡献者，为斜率优化部分提供参考。